引言
在人工智能和科學計算中,指數函數的計算無處不在——從神經網絡的激活函數到機率分布的計算。然而,為什麼我們總是使用自然底數e而不是更直觀的10或計算機底層的2?當這些計算遇到極值時,又如何處理數值溢位問題?本文將深入探討這些基礎但關鍵的數值計算概念。
ㄧ. 指數函數底數的選擇:e、10、2的數學意義
數值計算、機率或指數函數時,「為什麼總是用 “e" 而不是 “10″ 或其他底數如電腦中底層的 “2″ 進位運算」我來完整說明:
1. e 為什麼「自然」
- 定義:$e \approx 2.718281828…$是一個無理數,也是數學上稱為「自然對數的底(base of natural logarithm)」。
- 常見的定義方式有幾種:
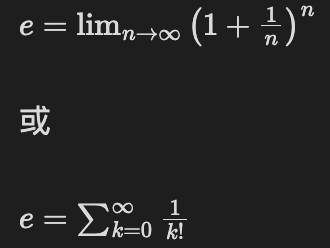
之所以叫「自然」,是因為在用 e 當底數的指數函數與對數函數,會出現非常自然、簡潔的數學性質:
(1) 導數與積分最簡單
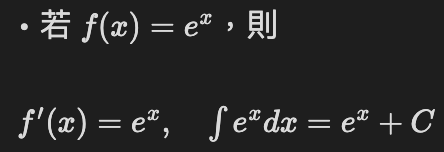
→ 它的變化率等於它本身,沒有額外常數,這在數學、物理、統計都很重要。

→ 就多了一個 $\ln(10)$的常數,計算起來不自然。
(2) 對數運算簡潔
- 自然對數 $\ln(x)$ 是 e 為底的對數。
- 它有簡單的導數:

如果是以 10 為底的$\log_{10}(x)$,則:

(3) 指數成長 / 複利公式
- 複利極限:一年 n 次複利,利率 100%:
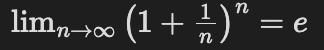
→ 所以 $e^x$ 自然地描述連續增長(人口成長、放射性衰變、利息等)。
2. 十進位(10)的直觀性與量級
- 十進制對數(log base 10) 常用在工程、日常計算:
例如聲音分貝(dB)、地震規模、pH 值、科學記號等。
因為人類日常習慣 10 進制,方便表示「量級(order of magnitude)」。
3. 電腦數值計算中為什麼不用 10 而以 2 為底數
- 電腦的浮點數設計(IEEE 754)是 以 2 為底數的科學記號(binary scientific notation),
例如:
1.1011_2 x 2^k
- 不管數學公式寫 $e^x、10^x$,電腦內部其實都會轉換成「以 2 為底的指數運算」,再乘上常數修正。
- 硬件實現:二進制狀態對應電路的開/關
- 位運算效率:$2^n$ 對應簡單的位移操作
二. 數值計算中 underflow(底溢) 和 overflow(上溢 / 溢位) 的概念
- Overflow(上溢):運算的結果超出該數值格式能表示的最大(絕對)值範圍,常見結果是得到 ±∞(浮點)、或整數發生「捲回/未定義行為」。
- Underflow(底溢):運算的結果的絕對值非常接近 0,小到超過該格式能以「標準化(normal)」表示的最小正數,會變成 次正規(subnormal/denormal) 或直接被表示為 0(在某些環境會被「flush to zero」)。Underflow 常伴隨精度喪失(有效位數顯著減少)。 浮點數(IEEE 754)核心機制(為何會發生) IEEE 754(單精度 float32 / 雙精度 float64)格式由三部分組成:符號位、指數位(biased exponent)、尾數(significand/mantissa)。
- 如果結果的指數太大(超出最大可表達 exponent),就 overflow → ±Inf 或 NaN(若為非數運算)。
- 如果結果的指數太小(絕對值太接近 0),會先變成 subnormal(失去隱含的領先 1),再更小則變成 0(即 underflow)。subnormal 可避免「突降為零」,稱為 gradual underflow。
- 還有特殊值:+0, -0, +Inf, -Inf, NaN。
2. 常見 IEEE 754 範例數值:
- float32(單精度)
- 最大有限值 ≈ 3.4028234663852886e+38
- 最小正規(normal) ≈ 1.1754943508222875e-38
- 最小 subnormal ≈ 1.401298464324817e-45
- float64(雙精度)
- 最大有限值 ≈ 1.7976931348623157e+308
- 最小正規 ≈ 2.2250738585072014e-308
- 最小 subnormal ≈ 4.9406564584124654e-324 (上面數值是 IEEE 754 的標準常數,目的是讓你有量級概念)
3. 整數溢位(與浮點不同)
- 固定位元的整數(例如 32-bit signed)有明確最大/最小:INT32_MAX = 2^31-1 = 2147483647,INT32_MIN = -2^31 = -2147483648。
- Unsigned:溢位通常會以模 2^n 的方式捲回(wrap-around)。
- Signed 整數溢位 的行為依語言而異:在 C/C++ 中 signed 溢位是 未定義行為(UB);在 Java、C# 等多數語言則是以二補數「捲回」或提供檢查 API(例如 Java 的 Math.addExact 會拋例外)。Python 的 int 則是任意精度,不會發生溢位。 Overflow / Underflow 的實際後果(為何重要)
- 結果變為 ±Inf 或 0 會導致後續計算完全錯誤(例如分母為 Inf、除法產生 0/0 → NaN)。
- 隱性錯誤:有些情況下溢位/底溢不會立刻崩潰,但會使演算法結果大幅偏離(難以偵測的 silent error)。
- 效能:處理 subnormal(denormal)數在某些 CPU 上會很慢;很多平台提供「flush-to-zero」選項來換成 0(以換取效能但犧牲精度)。
三. 電腦內部的常數修正 和 正規(normalized)/ 次正規(subnormal/denormal)
1.「常數修正」在數值函數實作上的意思
以 $a^x$ 為例(包含 $10^x$):常見作法是把它轉成以 2 為底的形式再計算,因為 IEEE 浮點最後是以 $2^{\text{exponent}}$ 儲存。
常見變形:

實作步驟:
- 計算 $y = x \cdot \log_2(a)$(或 $t = x \cdot \ln(a)$ 再做 exp)。
- 將 y 做 range reduction:拆成整數部份 k(要放到 exponent)和小數部份 r(放到尾數逼近):
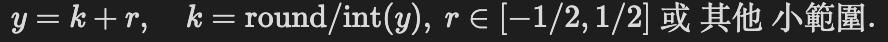
- 計算 $2^r$(用多項式或表查 + 多項式修正),最後結果是 $2^k \cdot 2^r$。
- 把 $2^k$ 對應到浮點的 exponent 欄位,把 $2^r$的值放進 significand(尾數)並做四捨五入 → 得到最終浮點數。 「常數修正」指的就是第(1)步和第(2)步所用到的常數(像 $\ln 2, \log_2(a), \ln a$)的乘法與拆分。在有限位數浮點中這些常數本身只能近似儲存,會造成微小的四捨五入誤差;為了把誤差壓到最低,實作會採用高低位拆分(hi/lo decomposition)來做精準的 range-reduction(見下)。
2. range-reduction 與常數拆分(hi/lo)的關鍵性
range-reduction 要把 $y = x\cdot\log_2 a$ 拆成整數 k 和小數 r。若直接做 $r = y – kln2$,因為 $kln2$ 可能很大,浮點運算中會有相減的捨入誤差(catastrophic cancellation)。實作常見策略:
- 把常數拆成兩部分:$ln2_hi$ 與 $ln2_lo$,滿足 $ln2 = ln2_hi + ln2_lo$,使 $kln2_hi$吞掉大部分,而 $kln2_lo$ 用來做小修正,最後 $r = y – kln2_hi – kln2_lo$,減少相減誤差。
- 這類「拆成高位 + 低位」的技巧是 IEEE-libm、glibc、musl 等高品質數學庫常用的方法,目的是在做多次乘加與相減時把誤差控制在一個非常小的範圍內,否則誤差會導致錯誤的 k 值、進而造成錯誤的 exponent → 可能導致意料之外的 overflow/underflow。
3.正規(normalized)與次正規(subnormal)的角色
IEEE 二進位浮點(以雙精度為例)表示法大致:
- 正規數(normal):表示為 $(-1)^s \times 1.\text{fraction} \times 2^{e – \text{bias}}$,其中尾數有隱含的 leading-1。
- 次正規(subnormal / denormal):當 exponent 欄位全 0(special case),表示為 $(-1)^s \times 0.\text{fraction} \times 2^{1-\text{bias}}$。也就是沒有隱含 leading-1 —— 意味著當值進入 subnormal 範圍時,可用的有效位數會減少(相對誤差變大)。 功能上:
- subnormal 使得從最小正規數到 0 之間不是一個斷崖,而是漸進式地遞減(gradual underflow)。這避免某些運算突然由非零變成精確 0,而導致劇烈錯誤。
- 代價:subnormal 的相對精度變差(有效位數少),且在許多處理器上處理 subnormal 會比較慢(硬體需要額外的 microcode 或軟體路徑)。
4. 在函數實作中 overflow / underflow 的產生機制
以 exp(x)(計算 $e^x$)為例說明:
- overflow(上溢):若 x 足夠大,使得 $e^x$ 超過該格式能表示的最大有限值$(double ≈ 1.7977\times10^{308})$,最後會變成 +Inf。實務上 exp(x) 在 double 上會在 $x \gtrsim 709.78$ 時溢位(因此 exp(710) 通常得 Inf)。
- underflow → subnormal 或 0:若 x 很小負,$e^x$ 可能落在正規下限以下但仍大於零,這時會回傳 subnormal(若硬體/環境支援),再更小則 0。在 double 上,若 $x \lesssim -745$(約數量級),exp(x) 會直接 underflow 成 0;介於 -708 及 -745 的區間則通常會得到 subnormal。
- 實作如何決定要輸出 subnormal 或 0:當在計算過程中 k(range reduction 得到的整數 exponent)小到使最終 exponent 欄位低於最小正規 exponent 時,庫會把尾數做位移以形成 subnormal,或若 shift 太大導致所有尾數位都移掉則得到 0。 常數修正(range-reduction 的乘法/相減)決定了 k 與 r。若 k 超出範圍就 overflow;若 k 小到使 exponent < min_normal,則產生 subnormal/zero(underflow)。
5. 次正規(subnormal)帶來的實務影響
- 精度變差:subnormal 沒有隱含 leading-1,相對誤差(relative error)會成為很大的數(比正常情況差很多)。
- 性能問題:在一些 CPU(尤其舊的 x86 SSE/AVX microcode、某些 ARM 核心)中,subnormal 的處理路徑比正常數慢很多(可能導致 pipeline stall)。因此有些應用會選擇「flush-to-zero(FTZ)」把 subnormal 直接當成 0,以換取效能(但會丟掉精度)。
- 例外/旗標:依 IEEE 754,若結果是「tiny 且 inexact」,會觸發 FE_UNDERFLOW(同時可能也觸發 FE_INEXACT);若結果超出 max,會觸發 FE_OVERFLOW。
4.工程上常用的避開或處理策略
- 在進行 exp/pow/log 等之前先做範圍檢查/clamp:例如$if (x > X_MAX) handle_overflow; if (x < X_MIN) handle_underflow;$。
- 用範圍縮放(scaling):對輸入或中間結果乘/除以 $2^n$ 把值帶到正常範圍,完成運算後再乘回。這可以避免 intermediate 進入 subnormal 範圍。
- 用對數域(log domain)運算:當處理機率乘積或非常小的乘法時(例如很多機率相乘),改用 sum(log(…)),避免直接 underflow。
- 使用數學庫的穩定實作:像 $expm1(x)(計算 e^x-1)$在 x ~ 0 時更精確;$log1p(x) 在 x ~ 0$ 時更精確。好的標準庫 implementations 已經處理好多 edge cases。
- 在效能敏感但可接受精度退化的情況下啟用 FTZ/DAZ:把 denormals 轉成 0,避免慢路徑,但要注意精度後果。
- 如果非常需要極端範圍與精度,使用更高精度類型(quad, MPFR, long double, arbitrary precision)來避免上/下溢。
5. 舉個簡單數值範例
- $double max ≈ 1.7977\times10^{308}$。若你寫 $exp(710)$,大多數標準庫會回傳 $Inf(overflow)$。
•$double 最小正規 ≈ 2.22507\times 10^{-308}。 exp(-709)$大概會落在正規界限附近;$exp(-740)$ 常常會落到 subnormal 或 0(視精確值而定)。
- float32(單精度)上,exp(89) 會 overflow(因為 float32 的最大約 $3.4\times10^{38},ln ≈ 88.7)$。
(以上閾值是常見近似值,實作細節會因平台與 libm 的不同而略有差別。)
6. 用常數拆成 hi/lo 與 overflow/underflow 的直接關係
- 常數拆解是為了 把 range-reduction 的殘差 r 算得精準,避免因為 r 的誤差把原本屬於 normal 結果的 k 算錯,導致本來應該是 normal 的結果錯誤地被分類為 overflow 或 underflow(或反向)。
- 換句話說:若 range-reduction 捨入太粗,整數 k 可能會「偏一格」,導致最終的 exponent 欄位錯誤 —— 也就可能把本來在 normal 範圍內的一個結果誤判為要設定為 subnormal 或是 overflow。因此高品質實作會做 hi/lo 拆分來把這種情況降到很低。
7. AI計算中的特殊考量
深度學習中的數值問題
Softmax函數的穩定計算:

梯度消失與爆炸:
使用梯度裁剪防止梯度爆炸
採用殘差連接和批正規化緩解梯度消失
四. 結論
- 當你在程式寫 $e^x、10^x、或 a^x$時,電腦通常會把這些運算轉成「以二為底/二進位形式」去計算(range-reduction + 多項式逼近 + 指數/尾數重建)。
- 在把理想的實數結果「打包成 IEEE 浮點(二進位)表示」時,如果指數太大就變成 Overflow(→ ±Inf);若太小則會變成 subnormal(次正規)或 0(underflow)。
- subnormal 是用來做 漸進式(gradual)底溢 的機制:能表達比最小正規還小的數,但精度與相對誤差大幅下降。
- 實作上,為了避免或控制overflow/underflow,數值庫會做常數拆分(hi/lo)、尺度調整(scale)、以及特別的 range-reduction/重建,並且在必要時把結果做「轉換成 subnormal 或 flush-to-zero」,或用其他穩定演算法回避。
指數函數計算中底數的選擇體現了數學理論與計算實踐的完美結合:e的自然性來自其微積分性質,10的直觀性服務於工程應用,而2的效率源於計算機架構。理解overflow和underflow機制對於設計穩健的數值算法至關重要,特別是在AI這樣對數值穩定性要求極高的領域。
隨著AI模型規模的持續增長,數值計算的挑戰將更加嚴峻。掌握這些基礎概念,是開發高效、穩定AI系統的必要基礎。
參考資料
理論基礎
- Higham, N. J. (2002). Accuracy and Stability of Numerical Algorithms (2nd ed.). SIAM.
- Muller, J. M., et al. (2018). Handbook of Floating-Point Arithmetic (2nd ed.). Birkhäuser.
- Goldberg, D. (1991). What every computer scientist should know about floating-point arithmetic. ACM Computing Surveys, 23(1), 5-48.
IEEE 754 標準
- IEEE Computer Society. (2019). IEEE Standard for Floating-Point Arithmetic. IEEE Std 754-2019.
- Kahan, W. (1996). IEEE Standard 754 for Binary Floating-Point Arithmetic. Lecture notes, UC Berkeley.
數值算法實現
- Tang, P. T. P. (1989). Table-driven implementation of the exponential function in IEEE floating-point arithmetic. ACM Transactions on Mathematical Software, 15(2), 144-157.
- Gal, S., & Bachelis, B. (1991). An accurate elementary mathematical library for the IEEE floating point standard. ACM Transactions on Mathematical Software, 17(1), 26-45.
AI與深度學習中的數值問題
- Micikevicius, P., et al. (2017). Mixed precision training. arXiv preprint arXiv:1710.03740.
- Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press. (Chapter 4: Numerical Computation)
開源實現參考
- GNU C Library. Mathematical Functions. https://www.gnu.org/software/libc/manual/html_node/Mathematics.html
- Intel Math Kernel Library (MKL). Vector Mathematical Functions.
- NVIDIA cuDNN Library. Deep Neural Network Library.
歷史與發展
- Knuth, D. E. (1997). The Art of Computer Programming, Volume 2: Seminumerical Algorithms (3rd ed.). Addison-Wesley.
- Forsythe, G. E., Malcolm, M. A., & Moler, C. B. (1977). Computer Methods for Mathematical Computations. Prentice Hall.






發表留言