Google 與 OpenAI 近日宣布,他們開發的 AI 模型在全球頂尖「國際數學奧林匹亞」(IMO)數學競賽中,首度雙雙奪金。對於創造數學的人類,更要有對此的重要性更有體悟,伽利略認為研究自然時應該遵循某個數學模型, 數學符號就是上帝用來書寫自然的統一語言。它們提供了一種簡潔、精確且國際通用的方式來表達數學概念和關係,對於現在不只有助於數學的發展和溝通,更是讓我們了解AI 語言模型的運作概念。
我以GB3102.11-1993 符號集合為基礎,我將分成 五個層級(重要性遞減),並在每一層中依實際在AI模型中的使用頻度與結構性依賴程度進行排列。
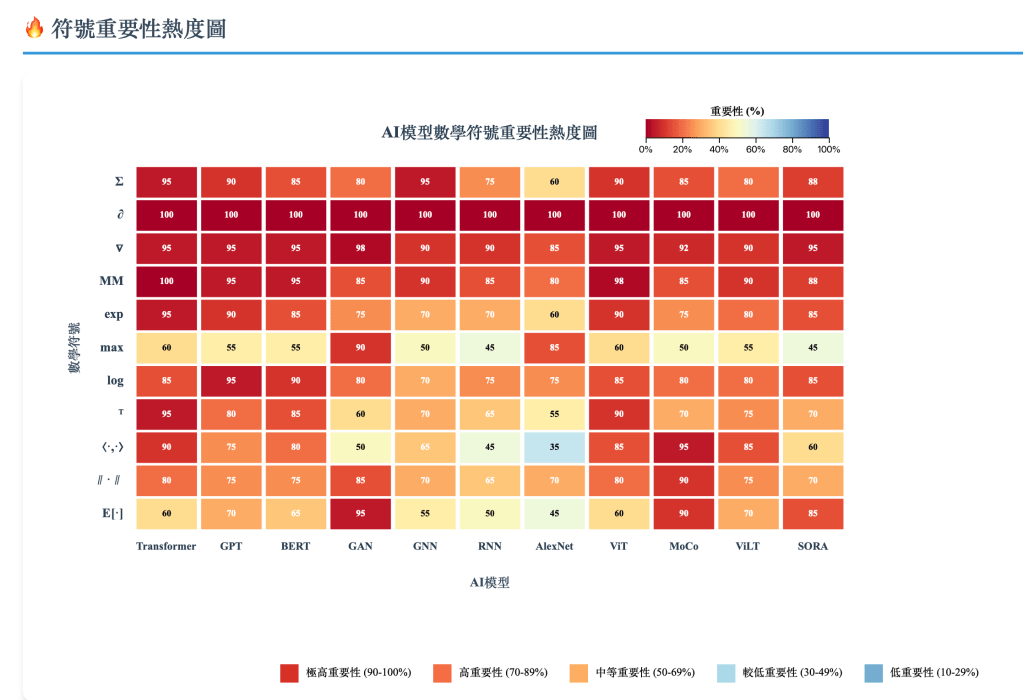
第一級:基礎運算與優化核心符號(必備基礎)
| 符號 | 定義 | AI 模型關聯 |
|---|
| Σ | 求和符號 | 注意力加權(Transformer)、損失累積(GPT、GNN、RNN)、對比學習(MoCo) |
| ∂ | 偏導數 | 反向傳播梯度計算;GAN 梯度懲罰項;擴散模型分數函數 |
| ∇ | 向量梯度算子 | 最優化(Gradient Descent/Adam),SORA中分數匹配 |
| AB(矩陣乘法) | 線性映射 Y = XW + b | Q、K、V計算;線性層;ViT patch Projection |
| exp/e | 指數函數 | Softmax;Sigmoid;擴散噪聲調度 |
| max/min | 最大/最小取值 | ReLU;MaxPooling;Minimax 遊戲(GAN) |
| log/ln | 對數 | Cross Entropy;JS/KL散度;語言模型 Log Likelihood |
| argmin / argmax | 最小/最大參數索引 | MLE、GAN 對抗目標;Transformer loss 最小化 |
第二級:線性代數與向量空間符號(深度模型運算核心)
| 符號 | 定義 | AI 模型關聯 |
|---|
| ⊤(轉置) | QKᵀ、矩陣轉置 | 注意力分數計算;權重矩陣轉置 |
| ⟨·,·⟩、· | 內積 | Query-Key 相似度;對比學習(MoCo) |
| ∥ · ∥ | 向量/矩陣範數 | Regularization、Normalization、Lipschitz 約束 |
| ⊗ | 張量積 / 多頭拼接 | Multi-Head Attention;交叉模態特徵拼接(ViLT) |
| ⊛ / ∗ | 卷積 | CNN / AlexNet;ViT patch 等價卷積思想 |
| ∘ | Hadamard 逐元素乘積 | LSTM/GRU Gate;Attention mask |
第三級:概率與統計符號(生成與自監督模型之基礎)
| 符號 | 定義 | AI 模型關聯 |
|---|
| E[·] | 期望值 | GAN Loss;Contrastive Loss;小批量梯度期望 |
| **P(·), P(· | ·)** | 機率 / 條件機率 |
| KL(p‖q) | Kullback-Leibler Divergence | VAE;分佈匹配;對比學習评价基準 |
| ∏ | 連續乘積 | 自回歸語言模型 $P(x_{1:T})=\prod_{t=1}^TP(x_t |
| ≈ 、 ∼ | 近似、分佈關係 | 擴散模型分佈近似;GAN 分佈擬合 |
| δ | Kronecker δ | One-hot、位置索引、節點身份(GNN) |
第四級:微積分與泛函符號(高階建模與聯繫)
| 符號 | 定義 | AI 模型關聯 |
|---|
| ∫ | 積分符號 | 連續分佈期望;變分下界(VAE / SORA) |
| sup / inf | 上下確界 | 生成對抗學習極值估計 |
| → | 極限, 收斂 | 參數收斂;訓練過程趨近最佳 |
| diag | 對角矩陣 | Attention Mask;權重初始化 |
| sigmoid σ | S 型函數 | GAN 判別器輸出;門控機制(GRU/LSTM) |
第五級:結構與集合符號(形式化表示)
| 符號 | 定義 | AI 模型關聯 |
|---|
| ∈ / ⊆ / ⊂ | 元素/子集 | 訓練資料定義;鄰居節點 (GNN);字彙表 (NLP) |
| ∪ / ∩ | 集合聯集/交集 | 多資料源融合(ViLT);異質圖訊息整合 |
| dim | 維度符號 | Transformer Head 維度、ViT patch 維度 |
| ⊕ | 向量拼接 | 多模態拼接;Embedding 合併 |
| Id / I | 恒等映射 / 單位矩陣 | 殘差結構 $y=F(x)+x$ |
| ∀/∃ | 全稱量词/存在量词 | 邏輯符號,表示“對所有”或“存在”,用於形式化约束 |
常見符號多重意思對照表
| 符號 | 數學 (幾何/分析) | 統計 | 機器學習 / 深度學習 |
|---|
| π | 圓周率 3.14159… | 機率參數 P(y=1),或類別機率 πj | Logistic regression 中成功機率;Softmax 機率分佈 |
| p | 變數、質數 (數論) | 機率 p(y),p-value | 常用來表示機率 (p(y |
| ϕ | 黃金比例、角度 | Normal 分佈密度函數 ϕ(x) | Feature map (核方法),高斯基底函數 |
| θ | 角度 | 參數 (如 θ 表示分佈參數) | 模型參數 (權重+偏置),f(x;θ) |
| μ | 測度 (measure)、集合論符號 | 期望值 (均值) | 資料分佈平均值、Batch Normalization 的均值 |
| σ | 總和符號(希臘 Σ 的小寫)、排列符號 | 標準差 | Sigmoid 函數 σ(z)=1/(1+e−z),也表示標準差 |
| λ | 特徵值 (eigenvalue)、波長 | 泊松分佈的平均數 | L2 正則化係數、學習率(部分文獻) |
| α | 角度、係數 | 顯著水準 (significance level) | 學習率 (learning rate),或注意力機制中的權重 |
| β | 系數、角度 | 線性迴歸係數 | 模型參數(權重),常在統計與 ML 中交替使用 |
| ρ | 密度、半徑 | 相關係數 (correlation) | 池化層 (rho-pooling) 符號(部分文獻),或 correlation |
| η | 數值分析中的步長 | 自然參數 (canonical parameter) | Learning rate(部分書籍),或神經網路輸入總和 z |
小結
- 同一個字母,在不同領域代表不同東西(例如 ππ 就有「圓周率」和「機率」兩種完全不相干的意思)。
- 統計 / GLM 喜歡用 π, μ, η, β。
- 機器學習 / 深度學習 喜歡用 p, θ, w, b, y^, σ。
- 讀論文時,要先判斷作者是站在哪個領域的傳統。







發表留言